这是一个创建于 1426 天前的主题,其中的信息可能已经有所发展或是发生改变。
傅立叶变换,有公式
F(t) = ∫fx * e^(-i* t * 2π) dx
t = 0,1,2,3 ... N
频率 t ,从做到又依次增加.
二维的情况, 应该也是,从左到右,从上到下,依次增加。 也就是 左上角是最低频,右下角是最高频。 类似于
1 2 3
2 3 4
3 4 5
但是看网上关于傅立叶变换的文章, 都是说,四周是低频,中间是高频(或者 四周是高频,中间是低频,然后平移变换,总之极值在中间。)
请问这个是什么原因呢? 网上人都这么说,应该是我理解错了。
还有,输出功率图的时候,是输出的振幅吧,复数的模,但我发现这个值很大,远远超过了 255 ( rgb 灰度值)。 这个是怎么处理的呢,谢谢。
非通信出身,见笑了 :)
1
1BF6oSYCD9ngBHo1 2021-10-19 18:56:28 +08:00
mark,最喜欢这种硬核的主题了
|
2
deplivesb 2021-10-19 19:01:03 +08:00 虽然我不会,但是我觉得如果论坛里能多一些硬核主题还是还是不错的
|
3
Rivers7 2021-10-19 19:31:08 +08:00
傅里叶变换平移不变性,平移到中心了,matlab 中 fftshift 函数就是这个功能
|
4
upojzsb 2021-10-19 19:33:43 +08:00 第一个问题:
计算机中使用的傅里叶变换并不是其连续形式,比如说一个 N 点(N=2^c, c 为整数)的信号 f[n]经过傅里叶变换后,会得到一个 N 点的复序列,其中第 k 个点(k=0, 1, ..., N-1)代表的频率是 k*fs/N,其中 fs 为信号的采样频率 我们假设信号 f 是一个实信号(由实数构成),那么可以由傅里叶变换的定义推导出 f(-\omega)=\bar{f}(\omega),即信号是共轭对称的,我们就可以根据正频率推导出负频率的信息,同时离散傅里叶变换是周期的,周期为 2\pi,所以我们可以根据[0,\pi]的信号推导出其它位置的信号 通过离散傅里叶变换得到的 N 个信号相当于对连续变换的 0~2\pi 的信号进行离散,所以第 0 个点代表 0 频率,第 N-1 个点代表 2\pi 频率,而\pi 到 2\pi 频率的信号相当于-\pi 到 0 频率的信号(根据周期性),-\pi 到 0 频率的信号相当于 0 到\pi 频率的信号的共轭(实信号的共轭性)所以在只考虑幅度的情况下,0~N-1 点的信号代表: 0, fs/N, ..., fs/2, fs/2-fs/N, ..., 0 0, 1, ..., N/2, N/2+1, ..., N-1 也就是从低频到高频再到低频 二维傅里叶变换同理: 低低 低中 低高 低中 低低 中低 中中 中高 中中 中低 高低 高中 高高 高中 高低 中低 中中 中高 中中 中低 低低 低中 低高 低中 低低 经过一个 fftshift 就变成中间低、四周高的形式 第二个问题: 我看二维傅里叶变换功率谱的时候一般会取个对数,看相对量 如果想更深入理解这些问题,可以参考: [1] 信号与系统 Oppenheim [2] 数字图像处理 冈萨雷斯 |
5
muhahaha 2021-10-19 21:41:13 +08:00 via iPhone
第一个问题上面已经有了相当全面的回答,第二个问题,功率一般采用 dBw 的形式,也就是楼上说的取对数,具体形式一般是 10✖️log(x)
|
6
shq619 2021-10-19 22:37:22 +08:00 via iPhone
复平面不是实数平面,所以高的在原点
|
7
necomancer 2021-10-19 22:44:58 +08:00 公式写错了,t->v
F(v) = \int f(t)Exp(-i 2\pi v t)d t 很显然当 f(t) 是实函数的时候 F(-v) = conj(F(v)),f 是复数的时候没有这个性质 然后离散傅里叶变换,加和变积分,F[k] = \sum_{m=0}^{N-1} f[m]Exp(-i 2\pi mk/N) 输出的数组按 k 为下标的话,F[0] 就是 \sum_{m=0}^{N-1} f[m]为整个信号的加和(积分),也是所谓的零频。如果数组长度是 N 的话,那么频率 k 最大到 N//2,这是 Nyquist 定理决定的,所以傅里叶变换后的数组 F[0~N//2] 是 0 频到最大频率,而 N//2~N 是负频率,即-N//2+1, ...., -1, 所以整个数组按照频率排序的话(偶数 N )的结构是 [0,1,2,...,N//2,-N//2+1,...,-1],而 fftshift 函数会将数组重排成为(按照频率)[-N//2+1,....-1,0,1...,N//2], 不难验证当 k=-N//2 和 N//2 时二者相等。正因为 Nyquist 定理决定了傅里叶变换后频率大小小于数组一半,即|k|<N/2,以及算法的原因,傅里叶变换的输出是先 0 频,再低频到高频,然后是负频率从高负频到低负频, |
8
1BF6oSYCD9ngBHo1 2021-10-22 21:45:44 +08:00
不懂傅立叶,但帮楼上完善下 tex 的公式显示:
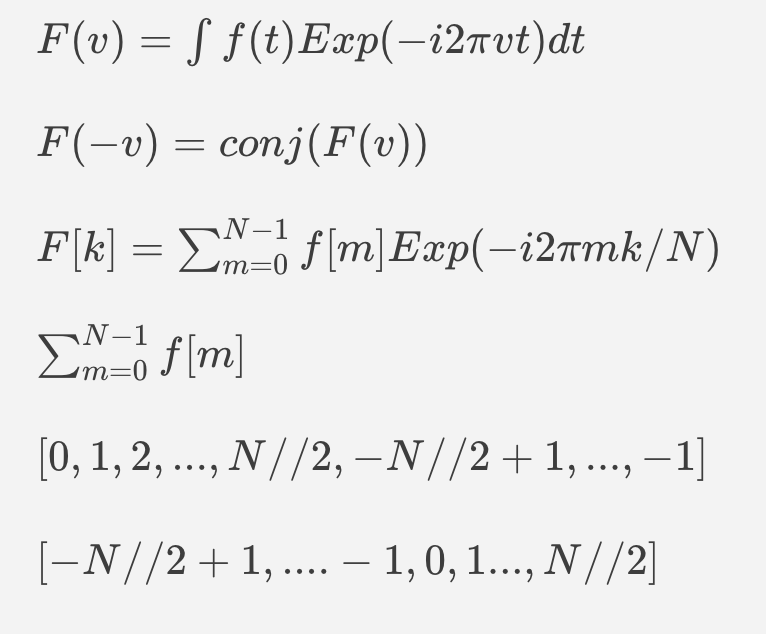 |
9
necomancer 2021-10-22 23:14:22 +08:00 昨天有事没详细写完,今天续上:考虑一个信号 f(t),变成一个长度为 N 的数组,数组标 i 其实和 t 是对应的,比如 t 是 0-T,那么 i=0,...N-1 对应 0,dt,2dt,3dt,....T-dt,其中 dt=T/N,但如果变成频率,首先,根据时频域倒数的关系,频率的单位是 1/T,第二,根据 Nyquist 定理,最大频率不能超过 0.5/dt,所以频率范围是 -0.5/dt~0.5/dt 。
程序里其实涉及的是数组下标的转换,在离散傅里叶变换里,输出数组的长度也是 N,比如下标 k 是 0,1,2,3,4,...N,那么按照定义,F[k] = \sum_{m=0}^{N-1} f[m]Exp(-i 2\pi mk/N),我们如果按照下标顺序也就是 0,1,2,3...计算的话,可以从 Exp(-i2\pi mk/N)里看出,当 k<N/2 时没有任何问题,我们可以让数组下标 0,1,....N/2 对应频率 0,1/T,2/T...0.5/dt,但当 k>N/2 时,按照数组下标对应规则,频率就超过 0.5/dt 了,这是不现实的,由于傅里叶变换因子存在对称性,即令 k=N/2+j (直接对应频率 0.5/dt+j/T),其中 j<N/2,那么变换因子 Exp(-i2\pi mk/N)=Exp(-i 2\pi m (1/2+j/N)) = Exp(-i \pi m -i2\pi mj/N),考虑 k'=j-N/2,则 Exp(-i2\pi mk'/N)=Exp(-i 2\pi m (j/N-1/2))=Exp(i \pi m -i2\pi mj/N),和 k=N/2+j 时是一样的(Exp(i \pi m)=-1^m,m 为整数),也就是说 k=N/2+j 对应的大于 0.5/dt 的频率其实等于一个负数频率即(j-N/2)/T=j/T-0.5/dt,这就是输出数组排序按照零频-低频-高频-负高频-负低频的原因。 |