这是一个创建于 2031 天前的主题,其中的信息可能已经有所发展或是发生改变。
N 年前面试阿里的时候有一道算法题不会做,后来一直念念不忘,在网络搜了一下也没找到答案,至今仍然没想出来...
题目是给一个方法 foo(),能以各 50%的概率随机返回 0 或者 1。问题是基于 foo()方法,实现一个 boo()方法,该方法能以各 10%的概率返回[0-9]中的一个数字。
感觉对受过相关训练的同仁来说应该不难,无奈本人对算法不是太在行 o(╥﹏╥)o
1
gaobing 2020-02-17 10:35:12 +08:00 那 0 或 1 拼数字 ,2 位的 数字 共 4 种排列,3 位的 8 种排列,4 位的 16 种排列 , 拿出 10 种排列指代 [ 0 -9] 这几个数字,剩下的 6 种排列不返回,重新计算随机数,直到出现 另外 10 种情况。
|
2
myd 2020-02-17 10:44:57 +08:00 楼上说的对。foo 方法其实相当于“抛硬币”。
连续抛四次硬币,所有的可能性一共有 16 种。如下: ``` '0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111' ``` bar()方法只需连续抛 4 次硬币,如果结果是上面 16 种可能中的前 10 种,就返回 0~9 对应的数字。如果结果是后 6 种,则抛弃结果并重新抛 4 次硬币。 |
3
stackexplode 2020-02-17 10:48:17 +08:00
想了一下
arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 用 foo()做二分查找 |
4
keith1126 2020-02-17 10:52:46 +08:00
|
5
slgz 2020-02-17 10:56:56 +08:00
马克
|
6
stackexplode 2020-02-17 11:00:14 +08:00
@keith1126
那就用[0-15]做二分。。 |
7
keith1126 2020-02-17 11:02:25 +08:00
|
8
zhaorunze 2020-02-17 11:03:57 +08:00
@stackexplode 这跟二分没啥关系吧
|
9
learnshare 2020-02-17 11:05:09 +08:00
foo -> 0/1
boo -> 四位二进制转十进制 #1 #2 已经讲明白了 |
10
stackexplode 2020-02-17 11:05:47 +08:00
@zhaorunze 1 分钟想个解法而已,只要概率是对的,没有什么有没有关系的
|
12
zhaorunze 2020-02-17 11:12:16 +08:00
@stackexplode 问题是这解法没用到二分的思想啊,就是 9 楼说的进制转换
|
14
churchmice 2020-02-17 11:15:43 +08:00
2 楼说的方法没毛病,这是好久之前的题目了,十年前找工作的时候我就看过
|
16
stackexplode 2020-02-17 11:19:42 +08:00
@zhaorunze 解决问题不一定要那么僵化的一定要用标准答案吧铁子,问题本质就是把 1/2 转换到 10%,二分绕了一圈,其实对 1-16 做二分恰好就是 0000-1111 的二分,确实不是完美答案,但也只是想的时候绕了一下而已
哪里有什么二分思想,二分思想就是概率思想 |
17
haha370104 2020-02-17 11:27:52 +08:00
要求有限步的话,其实知乎有一个类似于这个问题的讨论,做不到
不要求有限步的话 2 楼答案就对 |
18
JerryCha 2020-02-17 11:33:19 +08:00
1 楼的方法真是好
我净想条件概率去了 |
19
zhaorunze 2020-02-17 11:38:18 +08:00
@stackexplode 二分跟概率有啥关系,你说之前可以百度一下什么是二分查找。 这问题也不是概率转换的问题,1/2 怎么能转成百分之十?
|
20
freakxx 2020-02-17 11:42:37 +08:00
套路大概是这样, 先构建结果集,然后在结果集里面去构建。
[ [0, 1, 2, 3], [4, 5, 6, 7], [8, 9, x, x], [x, x, x, x], ] 抽象看成 rand(x) --> rand(y) 2 - 4 - 16 rand(3) --> rand(10) 3 - 9 - 81 去掉[9][9]那么概率是一样的。 |
21
ytmsdy 2020-02-17 11:55:00 +08:00
@stackexplode 二分不对的,永远都无法得到 10%这个概率。
|
22
yiqunz 2020-02-17 12:19:51 +08:00
|
23
zhw2590582 2020-02-17 12:32:43 +08:00
得到的经验就是,凡是看到 0 和 1 出现的题目,就要联想到二进制解法
|
24
suiterchik 2020-02-17 12:40:46 +08:00
背后的数学原理是舍弃采样(或者其他的蒙特卡洛方法也行),给你一个硬币,别说均匀分布,高斯分布都能给你采出来
|
25
momocraft 2020-02-17 12:41:02 +08:00
假想有一个区间从[0,1)开始
每掷一次 foo()为 0 则取左一半,为 1 则取右一半,直到这个区间已经是某个 [0.1*n, 0.1*(n+1)) 的子集时,返回 n 从计算的形状上看也是一种二分。 全用浮点数计算时一定在有限步内结束,在这一点来说比需要重掷的稳定,不过不是严格等概率 |
26
shilyx 2020-02-17 13:01:10 +08:00
function foo() {
return Math.random() < 0.5; } function foo2() { for (;;) { let n = 0; for (let i = 0; i < 4; ++i) { n *= 2; if (foo()) { n += 1; } } if (n <= 9) { return n; } } } !function foo2_test(times) { let res = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ]; for (var i = 0; i < times; i++) { res[foo2()] += 1; } for (let i = 0; i < res.length; ++i) { console.log(times + "次调用中" + i + "的次数: " + res[i]); } } (10000); |
27
st2523684 2020-02-17 13:54:13 +08:00
类似加权调度算法
|
28
Mohanson 2020-02-17 14:03:17 +08:00 via Android
硬币连续抛掷 32 次得到一个随机 u32 数字,然后取余 10 即可.
|
29
wsssss 2020-02-17 14:17:17 +08:00
//随机 return 0 到 3
foo0_3(){ return foo() + foo()*2; } //随机 return 0 到 15 foo0_15{ return foo0_3() + foo0_3()*4; } main(){ //随机给 a 赋值,范围是 0 到 15,超过 9,再重新给 a 赋值; int a = foo0_15; while( 9 < a ){ a = foo0_15; } return a; } |
31
wsssss 2020-02-17 14:20:49 +08:00
//随机 return 0 到 3
foo0_3 () { return foo() + foo() * 2; } //随机 return 0 到 15 foo0_15 () { return foo0_3() + foo0_3() * 4; } main () { //随机给 a 赋值,范围是 0 到 15,超过 9,再重新给 a 赋值; int a = foo0_15; while ( 9 < a ) { a = foo0_15(); } return a; } |
32
lxy42 2020-02-17 14:21:24 +08:00
leetcode 有一道类似的题目, 使用 rand7 实现 rand10: https://leetcode.com/problems/implement-rand10-using-rand7/
解决方法是拒绝-接受采样: https://en.wikipedia.org/wiki/Rejection_sampling |
35
mahone3297 2020-02-17 15:18:11 +08:00
|
36
wutiantong 2020-02-17 15:37:34 +08:00
1 楼(&2 楼)的解法是正确且本质的,这里分享一些额外的思考:
1. 不可能存在一个有限步的解法(证明略) 2. 不一定要每组 4 次,也可以每组 5 次,每组 6 次,,, 3. 如果我们关注调用 foo() 方法的次数,那么每组 4 次的期望值是 6.4 次,而每组 5 次的期望值是 5.33333333 次 4. 每组 5 次的方案是调用 foo()方法次数(期望值)最少的方案 |
37
buxudashi 2020-02-17 16:11:57 +08:00
思考了一下,给个最优解吧。
有十个位置,每个位置被 0 或 1 占位。于是就有了 0000000000-1111111111 (即 0-9 共 10 个位置)得到一个数字 x 这个数字每右移 1 位,只要大于 0,接着右移,而右移的次数称为 k 这个 k 就是 0-9 中的一个数字。所以 foo( )随机取 10 次,这 10 次组成的 x 所取的 k,就是答案。 2 楼给的答案有个极端最差,就是无穷次运行 foo 都会在后面 6 个数字里,取不到数字的。 |
39
buxudashi 2020-02-17 16:31:30 +08:00
@epicnoob k 为 0,再右移,右移后 k+1 ;
这个 K 就是 x 最高位所在的位置。当位置在第 0 位时,经过上一次操作,k 变成 1. 答案是 k-1 呀,就是 0. 因为是右移,它就不是 1/1024,而是 1/10,因为一共才移 10 次 |
40
buxudashi 2020-02-17 16:37:56 +08:00
10 个位置,这题就变向的变成 了:
最高位为 1 为位置 t 的地方。t 为 0-9 中的某一个数字。求 t |
41
ifzzzh 2020-02-17 16:46:45 +08:00
@buxudashi #40 你相当于把 0 到 2^11-1 的范围分成了[0,2^0), [2^0,2^1), ..., [2^10,2^11),明显有问题啊
|
44
buxudashi 2020-02-17 16:59:13 +08:00
@ifzzzh 机会均等。
第 9 位,第 8 位,第 K 位,跟第 0 位,都是均等占有最高位。所以 要先右移 1 位,再跟 0 判断。 第 t 位只有 0 和 1 这两个数字。你仔细思考下。我说最高位 1 是方便你理解。其实最高位是 1 或 0 两个占位。你想好判断条件。这东西在 c 语言里玩的多。 |
45
wangyzj 2020-02-17 17:03:20 +08:00
random.randint(0,1)
random.randint(0,9) 这样不行吗? |
46
ifzzzh 2020-02-17 17:11:01 +08:00
@buxudashi #44 你不就说这个十位二进制数最高位是第几位就取几吗,问题是第 9 位为 1 的概率=1/2,第 8 位为 1 的概率=1/4。。。。2 楼就是标准的拉斯维加斯算法,你换各种表达方式要不结果是错的,要不跟 2 楼的没区别
|
47
ixx 2020-02-17 17:12:03 +08:00
取 9 次,返回 1 的个数
|
50
stevesun21 2020-02-17 17:17:59 +08:00
foo 方法就是一饿 bit 的产生器
0 ~ 9 的 bits 是 0000 ~ 1001 百分之十其实就是 0 = 0000 1 = 0001 2 = 0010 3 = 0011 4 = 0100 ... 9 = 1001 那么接发就简单了因为是要求实现一个固定的 10%比例那么伪代码如下 1. 初始化一个记录器,记录 0 ~ 9 2. 调用四次 foo 得到 0 和 1 的一个 4 为 bits 3. 转化为一个 Integer 4. mod 这个 Integer 和 9 5. 然后看看这个 mod 后的结果是否在记录器中 6. 如果在,则从记录器中删除并返回, 7. 如果发现操作之后记录器中无数了,那么从新用第一步初始化记录器 8. 如果第 6 步的结果不再记录器中,那么从第 2 步再来一遍。 |
53
GjriFeu 2020-02-17 17:23:44 +08:00
我看见了不公
|
54
hicdn 2020-02-17 17:35:35 +08:00
@ixx 结果是正态分布
10 万次结果 {0: 182, 1: 1824, 2: 6997, 3: 16299, 4: 24808, 5: 24418, 6: 16446, 7: 7166, 8: 1668, 9: 192} {0: 189, 1: 1737, 2: 6906, 3: 16301, 4: 24588, 5: 24732, 6: 16463, 7: 7095, 8: 1780, 9: 209} {0: 188, 1: 1815, 2: 7083, 3: 16476, 4: 24716, 5: 24353, 6: 16213, 7: 7140, 8: 1836, 9: 180} |
55
hicdn 2020-02-17 17:38:07 +08:00
@gaobing
@myd 1 楼和 2 楼方法,10 万次结果,分布是均等的。 {0: 9996, 1: 9950, 2: 10009, 3: 9875, 4: 9910, 5: 10112, 6: 9984, 7: 10075, 8: 10130, 9: 9959} {0: 9955, 1: 9974, 2: 10037, 3: 10000, 4: 9928, 5: 9899, 6: 9950, 7: 10024, 8: 10002, 9: 10231} {0: 9922, 1: 9949, 2: 10072, 3: 9922, 4: 10088, 5: 9917, 6: 9962, 7: 10206, 8: 10171, 9: 9791} |
56
Windsooon 2020-02-17 17:46:44 +08:00
我整理了一下我的思路,欢迎大家讨论 https://v2ex.com/t/645301#reply0
|
57
hitmanx 2020-02-17 17:49:44 +08:00
@buxudashi 你这个 K 越大,概率越小,不是均匀分布的。因为 k 要求前面 k-1 个数都是 0, 且自身是 1,即 1/2^k
|
58
wulin 2020-02-17 18:04:00 +08:00
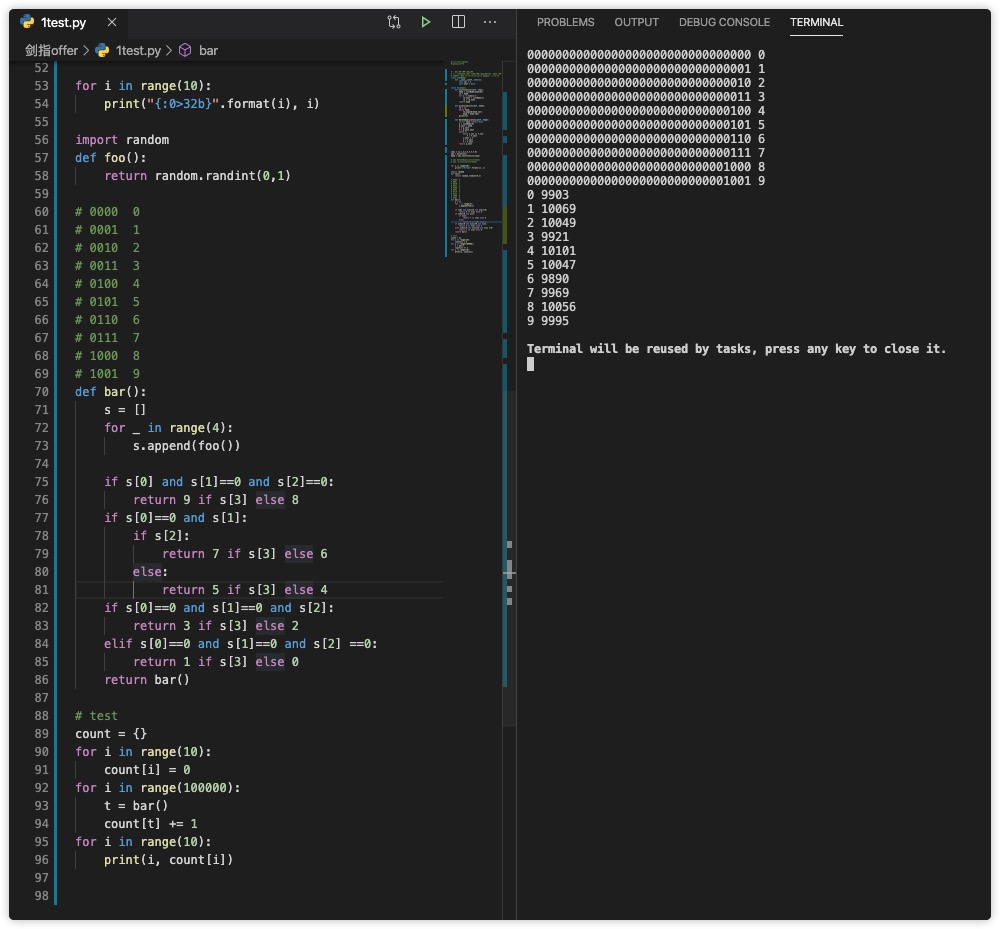
https://gist.github.com/wulinlw/b7f37207218b2973c0ba01e3f577629a 会多次递归... |
59
ixx 2020-02-17 18:15:36 +08:00
@hicdn #54 手动点赞,发完就想到问题了,50%的概率,都是 0 和都是 1 的概率应该远远低于 4、5、6 的概率所以不满足 10%的要求
 |
61
willhunger 2020-02-17 18:28:24 +08:00 via iPhone
Knuth 算法?
|
62
loryyang 2020-02-17 20:22:26 +08:00
上面楼太多了,不知道是否提到一个问题,这些方案从理论上都无法控制最差 case 下的时间。比如 16 中组合,拿 10 组,那么 6/16=37.5%的概率会重试,那么重试两次有 0.375^2,重试 10 次有 0.375^10 的概率,虽然很低,但是理论上依然存在。你无法控制这个最差 case。
另外我在想是不是做排列的时候,可以再多做一次,变成 32 种组合,选 30,那么有 2/30 的概率重试,重试概率大大降低了,虽然每次多计算一次 foo,但是相比较于重试的概率,应该不会亏 简单算一下(默认就算前两次),排列四次,期望 4*10/16 + 8*6/16 = 5.5, 排列五次:5 * 30/32 + 10 * 2/32 = 5.3。第二种期望的计算会少一些 |
63
loryyang 2020-02-17 20:25:02 +08:00
哦,我看到我的想法 @Windsooon 已经提到了,整理的还是挺完整的。我查了些资料,应该这就是最好的解了。看起来面试官也是准备了后手的,你提出 16 组合解之后,他应该会追问你:你觉得这个方案还有什么问题吗?
|
64
soy 2020-02-17 21:19:58 +08:00 算 4 次得到二进制数 x,(0<=x<16)
如果 x<10 返回 x 如果 10<=x<15 可以将(x-10)*2 再运算一个奇偶位返回 如果 x=15 重新计算 期望值 exp = 4*10/16 + 5*5/16 + (exp+5)*1/16 exp = 4.6 |
65
ic2y 2020-02-17 22:02:15 +08:00
@dazhangpan
可以换一个思路,我认为这个题目,考察的内容,非常接近 RC4 的流式加密算法,有个文章链接: https://www.cnblogs.com/gambler/p/9075415.html 题目中给出的 foo()函数 [产生 0-1 随机数] ,我们可以用来初始化 流式加密的 init 映射状态。随后的 随机数产生,可以完全不依赖 foo()函数,完全依靠流式加密的方式,产生概率 10%的 [0-9] ==============Java 代码如下================== package com.ic2y; public class RandomNumber { private static int MAPPING_LEN = 10; //映射 0-9 的 关系 private int[] mapping = new int[MAPPING_LEN]; private int i = 0; private int j = 0; public RandomNumber(){ //初始化 mapping,再进行打乱 for(int i = 0;i < 10;++i){ mapping[i] = i; } //shuffle 算法, for ( int i = MAPPING_LEN; i > 0; i-- ){ swap(getRandomLessTen(), i - 1); } } private int getRandomLessTen(){ int val; do { val = doGetRandomLessTen(); if(val < 10){ return val; } }while (true); } private int doGetRandomLessTen(){ int val = 0; for(int i = 0;i <4;++i){ val = val * 2 + foo(); } return val; } //已知的产生 0 1 随机数的 函数 private int foo(){ return (int)System.currentTimeMillis() % 2; } //外界调用 boo 产生 0-9 随机数 public int boo(){ i = (i + 1) % MAPPING_LEN; j = (j + mapping[i]) % MAPPING_LEN; swap(i,j); return mapping[(mapping[i] + mapping[j]) % MAPPING_LEN]; } private void swap(int l,int r){ int tmp = mapping[l]; mapping[l] = mapping[r]; mapping[r] = tmp; } public static void main(String[] args){ RandomNumber r = new RandomNumber(); int testNumber = 100000; int[] f = new int[10]; for(int i = 0;i < testNumber;++i){ ++f[r.boo()]; } float fTestNumber = (float)testNumber; for(int i = 0; i < 10;++i){ System.out.println(String.format("Num:%d Probability:%.2f count:%d",i,f[i] / fTestNumber,f[i])); } } } =======结果======= Num:0 Probability:0.10 count:9863 Num:1 Probability:0.10 count:10051 Num:2 Probability:0.10 count:10054 Num:3 Probability:0.10 count:10024 Num:4 Probability:0.10 count:10031 Num:5 Probability:0.10 count:9942 Num:6 Probability:0.10 count:10007 Num:7 Probability:0.10 count:9877 Num:8 Probability:0.10 count:10083 Num:9 Probability:0.10 count:10068 |
66
wizardoz 2020-02-18 17:11:53 +08:00
@learnshare 你这算法还没做到 10%的概率
|
67
wizardoz 2020-02-18 17:14:17 +08:00
@learnshare 好吧我错了,没细看 1#答案
|