V2EX › 程序员
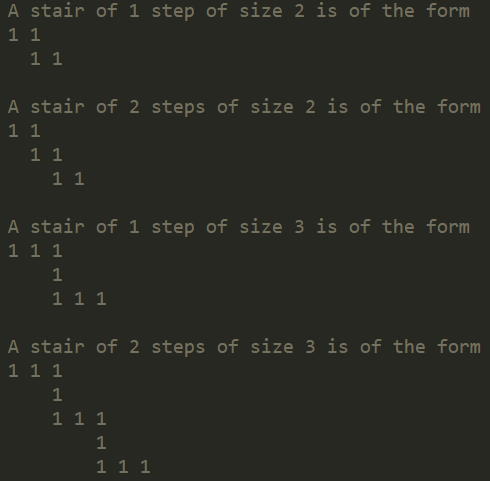
求助一道算法题。求思路。由一个 0 和 1 组成的矩阵,求出所有 1 构成的阶梯。
letianqiu · 2017-08-18 20:08:44 +08:00 · 4536 次点击这是一个创建于 2690 天前的主题,其中的信息可能已经有所发展或是发生改变。
初步发现 size * (steps + 1) - steps = n,如果对于每一个元素都枚举一遍,感觉复杂度非常高,而且会重复,比如 size 为 2 的可能是 size 为 3 的其中一部分。求指导
1
shard 2017-08-18 20:25:56 +08:00
动态规划
|
2
menc 2017-08-18 20:29:51 +08:00
这是一道回溯法的题啊,
只不过加了一个向右和向下的 step 必须一致的约束不是么 |
5
Magentaize 2017-08-18 20:40:58 +08:00
行最简形矩阵
|
6
shard 2017-08-18 20:44:37 +08:00 via iPhone
没审题,我沙壁。请无视
|
8
geelaw 2017-08-18 22:44:16 +08:00 via iPhone
预处理每个位置开始往右往下可以有多少个 1,然后递推找出每个位置是否是某个阶梯的结束位置
|
9
hezhe 2017-08-19 00:54:45 +08:00 via Android
能否使用 dfs?找到的点标记下,但有的点有又可能会出现新的阶梯中,要分类判断下。
|
10
hxndg 2017-08-19 02:49:43 +08:00
好久没做题了。。。总感觉回溯或者搜索都必须注意时间复杂度啊,总感觉会爆栈
|
11
Xs0ul 2017-08-19 03:42:38 +08:00 via Android
我想的居然是卷积,怕不是学傻了(
|
12
victor97 2017-08-19 09:42:38 +08:00 via Android
首先,每行每列求前缀和,可以快速判断某条线段是否全为 1。
枚举所有位置,再枚举长度,向左上方找。 因为不考虑重复,所以要找仅 1 step 的阶梯即可。 总复杂度 O(n³) |
13
letianqiu OP @victor97 需要考虑重复。当前我能想到的就是对每一个元素枚举,从 size 和 step 分别增长,找到存在的阶梯之后,比较是不是 map 里已有的 path 的其中一部分,如果是,就说明是重复的,放弃这条 path, 否则记录下 path,扔到 map 里。感觉复杂度至少 O(n^4)
|
14
victor97 2017-08-19 09:56:22 +08:00 via Android
是 起点相同,size 相同,step 不同 算重复吗,
还是我理解错了重复的意思? |
16
victor97 2017-08-19 10:57:42 +08:00 via Android
我的意思其实也是重复的只算一次。
从左至右,从上到下,枚举位置,那么只要判断左上方一个台阶就够了。 如果要记录位置长度,再找到满足要求的更新坐标;如果不记录位置长度,只找一阶的数量就是答案。 |
17
letianqiu OP @victor97 不是很明白你的意思诶。我算法水平太弱了。为什么只判断左上方一个台阶就可以。我的想法很初级,就是枚举每一个位置,往右下方走,size 从最小的 2 开始,step 从 1 开始,所有 step 找遍之后。size 增加。但是觉得这样有很多重复的。比如一个全都是 1 的 matrix,从( 0,0 )开始可以走到底,当从( 1,1 )开始走时,很多路径其实在( 0,0 )的时候都走过了, 属于无效的。
|
18
victor97 2017-08-19 11:26:47 +08:00 via Android 因为左上方的所有位置都是统计过的,如果发现能组成一阶台阶,要么是新出现的台阶,要么之前就已经是台阶了,只是长度 + 1,算重复。
|
19
letianqiu OP @victor97 明白了。不过你说的求前缀和有什么用,就算知道了某列或者某行全为 1,并不能说明什么啊。还是需要枚举每一个位置。
|
20
letianqiu OP @victor97 还有个问题,怎么区分是新台阶还是长度+1 的旧台阶。是不是和我原始的想法类似,开 map 保留所有已知的台阶构造,如果不是新台阶,那么当前位置(x, y)的上方(x-1, y)和左上方(x-1, y-1)是属于已经存在的台阶的构造的一部分,此时将原始台阶的长度+1,否则就是新台阶,加入 map
|
21
imn1 2017-08-19 12:13:56 +08:00
原矩阵把 行 中连续的 1 保留,其他置为 0,得到新矩阵 A
原矩阵把 列 中连续的 1 保留,其他置为 0,得到新矩阵 B AB 的交集(逻辑与)就是阶梯的角 后面自己推吧 |
22
imn1 2017-08-19 12:18:22 +08:00
楼上#21 说的不严谨,但原题也没有说清楚
#21 说的是 转角 还需要排除“断层” |
23
letianqiu OP @imn1 如果全都是 1 的矩阵,这么操作之后,并没有任何变化啊。要求就是 i 找出所有的形如图片中的台阶。觉得#18 说得有道理啊
|
24
imn1 2017-08-19 12:43:24 +08:00
@letianqiu
实际上我就是搞不清楚你原题中阶梯的定义 例如 11000 01000 01000 011111 这种是否也算阶梯 其实最简单的方法就是 把所有符合阶梯定义的图形都写出来,然后去矩阵中找交集(平移和竖移) 这里问题就是矩阵越大,那阶梯图形就越多,而且阶梯不明确定义横向最大连续和纵向最大连续的话,阶梯的变化很多 反正思路不应该是在矩阵中逐点“画”阶梯,而是把已知定义的阶梯整体在矩阵中匹配 |
27
letianqiu OP @mrcn 对啊。对于状态转移方程这题完全没有思路。目前觉得#18 楼的方法比较可行。#21 的方法对我来说太过于高深了。大致能理解他的意思,但是完全驾驭不了
|
28
victor97 2017-08-19 13:24:37 +08:00 |
29
victor97 2017-08-19 13:28:50 +08:00
|
31
letianqiu OP @victor97 大致明白了。受益匪浅啊。非常感谢啊。只是对于“另外,不需要用 map,每个位置记录以它为结尾的所有阶梯就行。”还有点点疑问。每个位置可能是不同 size 的阶梯的结尾,如果不开个 map 保存,如何能够记录。也许我没表达清楚题目要求,题目需要记录所有 size (宽度)下所有不同 steps (高度)的阶梯。所以我就想保存一个 map,key 是 size,value 还是一个 map,这个 map 的 key 是 steps,value 是阶梯的结尾位置的坐标。一个位置不可以出现在同一个 size 下,不同的高度的阶梯里。但是可以出现在不同的 size 的阶梯中。
|